12. PID Implementation Solution
def run(robot, tau_p, tau_d, tau_i, n=100, speed=1.0):
x_trajectory = []
y_trajectory = []
prev_cte = robot.y
int_cte = 0
for i in range(n):
cte = robot.y
diff_cte = cte - prev_cte
prev_cte = cte
int_cte += cte
steer = -tau_p * cte - tau_d * diff_cte - tau_i * int_cte
robot.move(steer, speed)
x_trajectory.append(robot.x)
y_trajectory.append(robot.y)
return x_trajectory, y_trajectory
Ok. With the integral term we're keeping track of all the previous CTEs, initially we set
int_cte
to 0 and then add the current
cte
term to the count
int_cte += cte
. Finally we update the steering value,
-tau_p * cte - tau_d * diff_cte - tau_i * int_cte
with the new
tau_i
parameter.
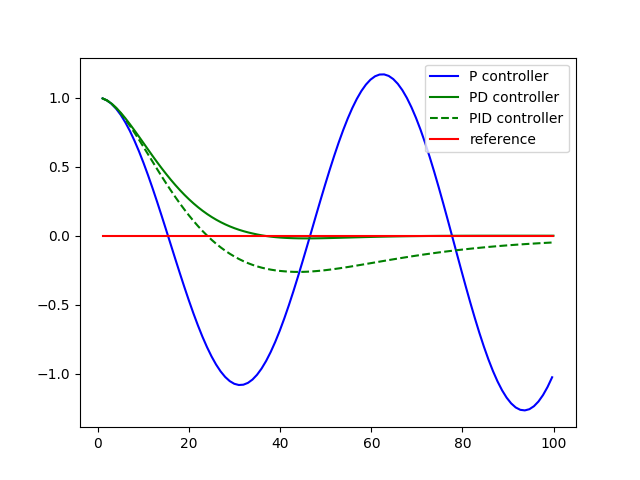
This may not seem all that impressive. PID seems to do worse than the PD controller! The purpose of the I term is to compensate for biases, and the current robot has no bias.
In the next programming quiz we'll add steering drift and revisit this graph.
PID Implementation Solution - Artificial Intelligence for Robotics